Copyright 2005 Full
Tilt Poker
November 29, 2005
(View all Online Poker
Lessons)
Poker Lesson: What's Your Starting
Hand Really Worth?
Author: Steve Brecher
Most players know that pre-flop position is important
in hold 'em. The earlier
your position, the more players there are behind you and, unless
you hold pocket Aces, the bigger the chance that one of them will
have a hand better than yours.
There is another aspect to position: It's better
to act after your opponent(s) rather than before. But for this
tip, I'm going to investigate the chances that a player behind
you will have a better hand.
There is no universal definition of what "better"
means when comparing hold 'em
starting hands. For this article, I needed some reasonable,
quantifiable criterion. So in the following, I'm assuming that
one hand is "better" than another if its showdown equity
is greater. A hand's showdown equity against another hand is the
average portion of the pot it will win across all possible combinations
of board cards. This is similar to the percentages that TV poker
programs display next to player hands when the players are all-in.
If you're interested in investigating this for yourself, there
are several free computer programs and websites which calculate
the showdown equities of user-specified competing hands.
For example, Ah 2d all-in pre-flop against Kc Qc
will, over all possible boards, win an average of 53.9% of the
pot. So the A-2 is the "better" hand against K-Q suited
by our definition. Obviously, it is not better for all purposes;
at a full table I'd usually open-raise in early position with
K-Q suited, but toss A-2 offsuit.
Given some specific hand category – such as
K-Q suited – we'll need to know the chance that a random
hand dealt from the remaining 50 cards will be "better."
This requires that we have a showdown equity calculation for each
of the 1,225 possible opposing hands and tabulate against how
many of them the K-Q suited has the worse (less than 50%) equity.
It turns out that 238 of the 1,225 possible opponent hands are
"better" in this sense. So we say that the chance of
a random hand being better than K-Q suited is 238/1,225 or 19.4%;
conversely, the chance that a random hand will not be better is
80.6%. This tabulation would be too tedious to do by hand. For
the example results below, I developed some simple software to
do the calculations.
Suppose that you are considering an opening bet
pre-flop. There are players yet to act behind you. I'll denote
the number of hands to play behind you as N. For example, if you're
on the button, then there are two hands - the blinds - behind
you, and N would be equal to 2. What is the probability that none
of some number of random hands will be better than yours? It is
the chance that one random hand will not be better than yours
multiplied by itself N-1 times, which is the same as saying it's
that probability raised to the Nth power. For example, if there's
a 40% chance that a random hand won't be better (i.e., a 60% chance
it will be better), then the chance that none of three random
hands will be better is 40% x 40% x 40%, or 0.4 to the 3rd power,
which equals 0.064. Hence, the chance that at least one of the
three hands will be better is 1.0 - 0.064 or 0.936 or 94%.
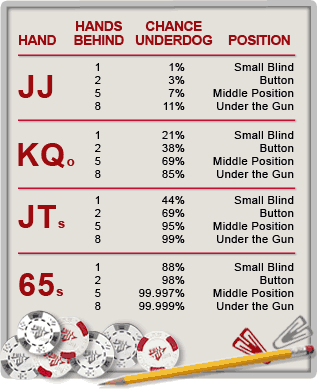
(source: http://www.fulltiltpoker.com/proLessons.php?lesson=37)
I think the most interesting thing about these numbers
is the difference between earlier and later positions. This is
something to consider when you're thinking of open-raising in
early position.
FullTilt
Poker Bonus Code
Also see Poker
Staring Hands for more help

Downloaded
from the World Wide Web on November 29, 2005:
http://www.fulltiltpoker.com/proLessons.php?lesson=37
|









